I never actually put my thesis anywhere on the internet. I finally had the energy to look back at it this week to start revising it into an actual publishable form and figured I'd throw it on here in case anyone wanted to see it. I finished this thesis up at the beginning of the pandemic, and I just haven't been quite ready to revisit that headspace until now! (I just looked at it for the first time in more than 8 months to convince myself it was not horrible.)
The official title is Partial Marked Length Spectrum Rigidity of Negatively Curved Surfaces, which will also probably be the title of the paper when I get my act together and submit it somewhere. Some of my earlier blog posts were on parts of the background:
The space of geodesics and the boundary at infinity in two blog posts:
I also talk about geodesic currents in these posts:
If you've seen me give a talk over the past year or two, I have probably told you about the marked length spectrum, geodesic currents, and/or why I care so much about loops on certain types of surfaces.
You can find my thesis on Google drive here or download it below.
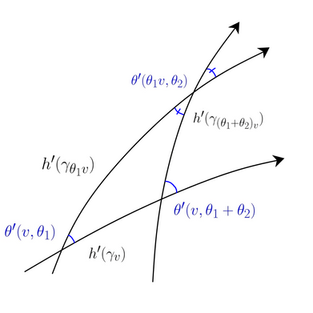
Below is a grid of the images in my thesis, provided without context. If something about my math is interesting to you and you want to talk, let me know!
