Last time, I talked about what geodesic currents are - very nice measures on the space of geodesics. An example I gave was of the closed orbit current. They're great - they're measures that weight the whole space based on lifts of a closed geodesic. All of the geodesic currents are not as easy to think about, but this next one is a little more like what I would come up with. A current that measures angle spread and how wide the set of geodesics is, in a sense.
The Liouville Current
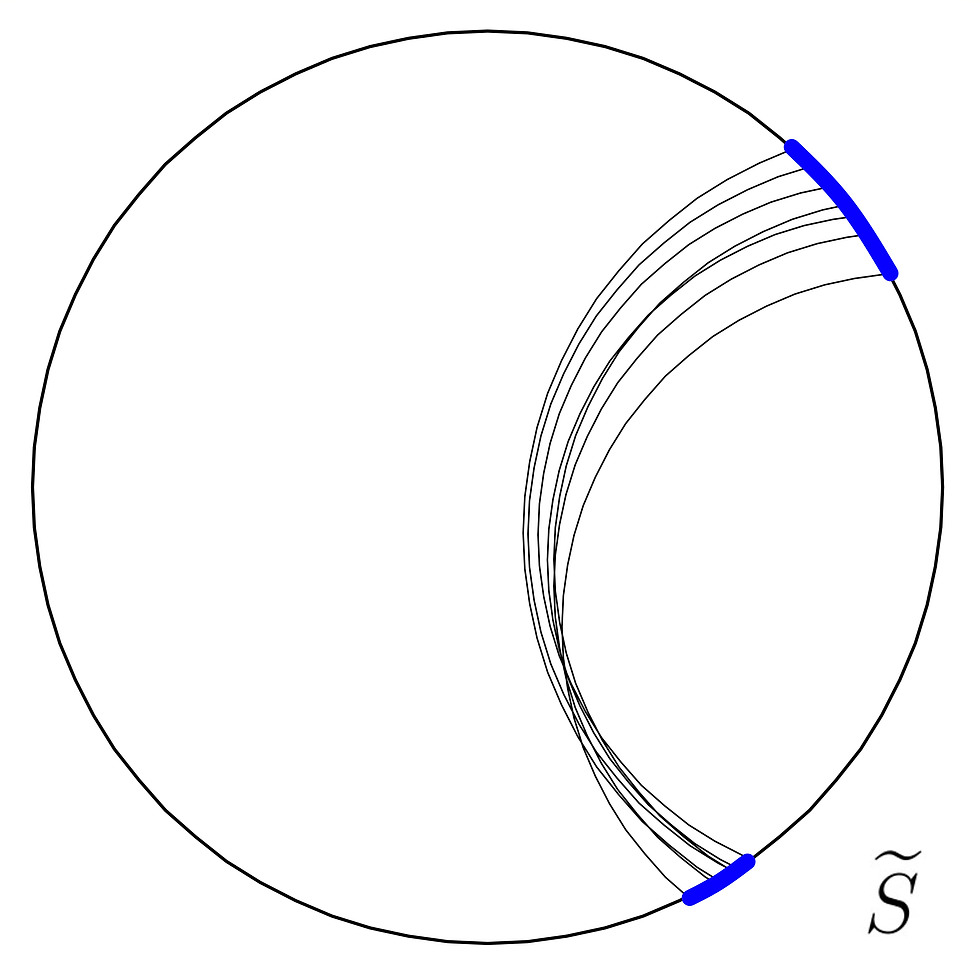
Just as a reminder of the kind of setting we're in; We have a surface S and we're looking at its universal cover. The space of unoriented geodesics is the space of geodesics on the universal cover with the metric inherited from the surface. A basis element in the topology is all the geodesics passing between two open sets on the boundary, like the blue sets on the picture to the right.
Now, even just from this picture, we can see that the set of geodesics doesn't look to be the same width everywhere. It's wider near the boundary than it is anywhere else, so we have to make a choice about where we'd like to measure the width. The same goes for the angles of the geodesics with relation to each other. So let's decide where to measure the width. Choose a geodesic that's transverse to all the geodesics in our set, call it T, and measure what length of T has nonempty intersection with our set. That is, how much time, t, it takes T to run through our set. Then, we pay attention to the angle each geodesic makes with T, like below. The transverse geodesic is in green, and we can see how time and angle are measured.
Now, to measure our set A, we integrate.
Definition: The Liouville measure of A with respect to a metric m is
Where the angle and time are as discussed above.
Some things to notice:
The metric determines how we measure angles, and so there is a Liouville current associated to each metric m.
If every geodesic in a set intersects T at the same angle, then it is a measure zero set.
A question that's begging to be asked here: What changes when we pick another transverse geodesic? How can we make a choice of of transverse geodesic T that's consistent? Well, it turns out that no mater what transverse geodesic you choose, the integral gives the same output! Another thing this tells us:
If the geodesics in a set all intersect at a single point, the set has measure zero. We can see this by taking T to be a geodesic that passes through that point.
If you're anything like me, the Liouville current seems more like information I would want to know, but the closed orbit currents from last time seem so much easier to handle. We can have the best of both worlds with the following result:
Proposition (Bonahon, 1991) Closed orbit currents and their real multiples are dense in the space of geodesic currents. (From The geometry of Teichmuller space via geodesic currents, Inven. Math. 33 (1991), 445–464.)
This means that we can approximate any geodesic current with a multiple of a closed orbit current! So, choose how close* you'd like to be to your current of choice. There exists a closed geodesic whose closed orbit current, or a multiple, is that close to that current.
*- close in the space of geodesic currents is in the weak-* topology. Given a current, and n real valued functions on the space of geodesics, and open ball around that current of radius episilon is
Next time, I'll talk about a tool that combines geodesic currents to give us more geometric information about our surface.